April 3, 2017: Correcting incorrect correction correctly
All text and images copyright Michael E. Lockwood, all rights reserved, unless otherwise noted.
Correction is a term that both helps describe the amount of departure from a sphere that a mirror has and also implies that the mirror is not spherical. Ellipsoids, paraboloids, and hyperboloids all have different amounts of correction. This means that the curve in the mirror changes from center to edge, and for the geometry of a paraboloid, this causes a point source at infinity (which is what a star is) to focus perfectly at the focal plane.
Strictly speaking, since a parabola is one very specific shape out of an infinite number of other shapes, I never really make a parabola, because no mirror is perfect. However, the goal is to have the mirror be as close to a parabola as is practical to make.
Enter a couple of mirrors that have crossed through my shop door recently.......
The first is a 20" that is undercorrected. That means that the outer zones of the mirror focus shorter than they should, and are therefore too "high". The center zones appear to be high, also. This mirror's surface has the shape of an ellipse, not a parabola. The plot below shows the error in the shape of the mirror, or the departure from the ideal parabola.
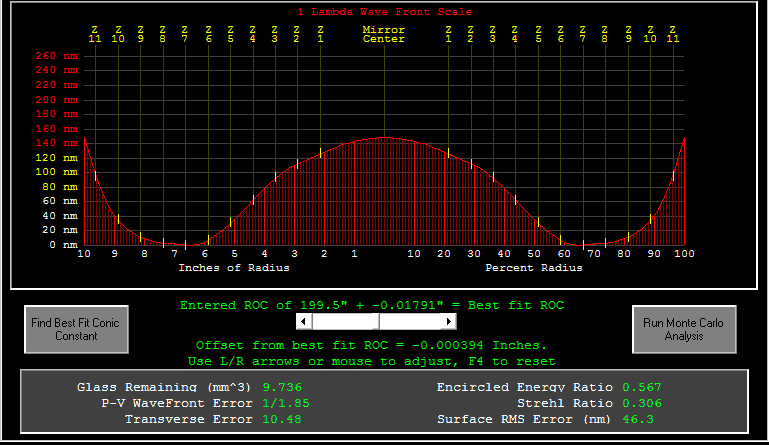
One key metric in the plot above is the transverse error. This means that light from some zone of the mirror is ending up ~10.5 airy disk radii from the spot where a perfect mirror would direct them. This means that a star image is much larger than the ideal, and under good seeing conditions detail is lost and smeared. The wavefront error is around 0.6 waves, also obviously not good.
Another mirror, a 16", displayed the opposite problem - it is overcorrected, and its outer zones focus too long. It is actually closer to a hyperbola. See error plot below.
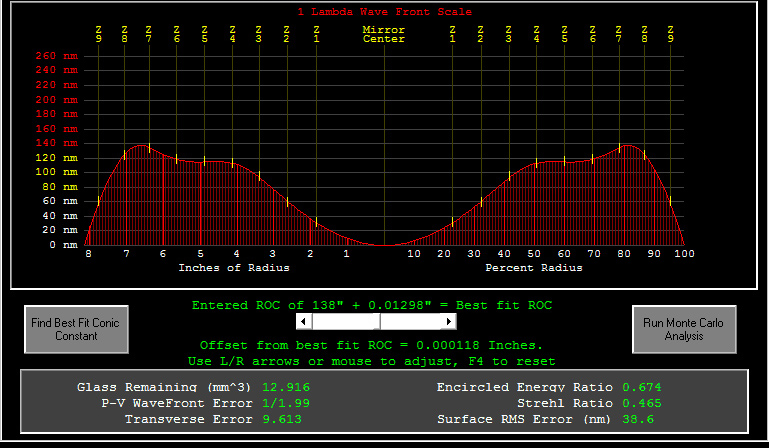
This mirror has a very similar transverse error - ~9.6 - so stars are bloated by approximately the same amount as the other mirror, but this time the outer zones focus too long rather than too short. Also the wavefront error is not too different, very close to 0.5 waves exactly.
Fixing the first mirror, the undercorrected one, is easier than the second, overcorrected mirror. Normally I try to start off with a mirror that is near a sphere, which means that it is very undercorrected. So, fixing an undercorrected mirror is somewhat like normal figuring, or the process of transforming a mirror that is nearly spherical to one that is nearly parabolic. Fixing an overcorrected mirror means reducing correction in the outer zones, which is not as simple as adding correction.
In any event, correction error is not a good thing. Sometimes undercorrection is done on purpose to help compensate for how the glass deforms/warps as it cools, because mirrors appear more corrected than they really are as they cool off. Figuring larger, thicker mirrors using the star test and no lab/bench testing often results in undercorrection. However, this is unwise and leads to poor performance after the mirror gets close to the air temperature. Overcorrection is worse, though, because the condition becomes even worse as the mirror cools off.
So, measuring correction is extremely important to making a good mirror. It is surprising that it is often quite far from the ideal. In cases like this where the mirrors are good figures of revolution (minimal astigmatism, etc.), the simplest tests, such as Foucault/knife edge testing, give a highly accurate measurement of the correction of the mirror, and the errors can be quite precisely corrected.
Please check back for future installments of "In the Shop".
Mike Lockwood
Lockwood Custom Optics



